Constraint checking for Sudoku
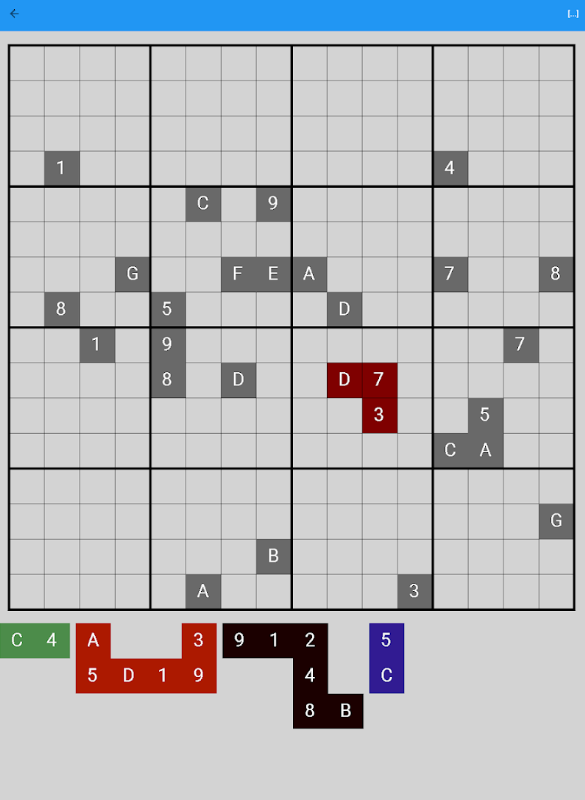
Extract from the report of my computer science degree
During the programming of Sudozzle, I had to find a way to code a grid checker and a sudoku creator.
I therefore worked on an algorithm to create a valid sudoku grid, respecting the constraints of the sudoku game and generating the numbers randomly, in order to obtain material useful for creating the game.
I looked for the most efficient ways of creating a sudoku grid. Sudoku algorithms are well-documented on the web, and offer a variety of mathematical alternatives.
The research led to understand that the methods used to check sudoku constraints had little impact on the efficiency of the algorithm. So I started by creating a brutforce method to enable for any given grid to check whether the numbers are unique in their rows, columns and regions.
For the grid-filling algorithm, I produced an initial version that simply randomly generated each number, validating it only if it met the row, column and region constraints at the time of installation. This type of algorithm seemed the simplest solution and had the advantage of being reliable. However, following various tests on my machines, the generation of a complete sudoku was definitely too long to be acceptable in an application. What's more, increasing the size of the sudoku, in particular to 16 by 16, made generation almost impossible, as it was too resource-intensive for the machines, with resolution times sometimes exceeding 30 seconds for a 16 by 16 sudoku.
I then turned my attention to the backtracking solution and the problems of satisfying algorithmic constraints. Backtracking is a specific type of programming for solving constraint problems, which consists in testing possibilities and, if a solution cannot be found, going back to the most recent problem to test another solution (See Figure above). In theory, backtracking avoids time-consuming generation. We have therefore created a program corresponding to this category of algorithms, using the lessons and examples we found. The backtracking solution proved more efficient both in terms of time and resource consumption. The generation of a complete 16-by-16-square sudoku is of the order of a tenth of a second. However, this algorithm was not very efficient when generating larger numbers, such as a 25 by 25 sudoku matrix. The resolution time was then in excess of 30 seconds, which is not acceptable for a mobile application.
My research turned to the work of Donald Knuth and sudoku generation algorithms inspired by the Dancing Links algorithm, a recursive search algorithm using trace feedback. However, this solution remained recursive and presented major difficulties when it came to generating a random grid.
For many reasons the backtracing algorithm seemed to be the best solution for Sudozzle.
During the programming of Sudozzle, I had to find a way to code a grid checker and a sudoku creator.
I therefore worked on an algorithm to create a valid sudoku grid, respecting the constraints of the sudoku game and generating the numbers randomly, in order to obtain material useful for creating the game.
I looked for the most efficient ways of creating a sudoku grid. Sudoku algorithms are well-documented on the web, and offer a variety of mathematical alternatives.
The research led to understand that the methods used to check sudoku constraints had little impact on the efficiency of the algorithm. So I started by creating a brutforce method to enable for any given grid to check whether the numbers are unique in their rows, columns and regions.
For the grid-filling algorithm, I produced an initial version that simply randomly generated each number, validating it only if it met the row, column and region constraints at the time of installation. This type of algorithm seemed the simplest solution and had the advantage of being reliable. However, following various tests on my machines, the generation of a complete sudoku was definitely too long to be acceptable in an application. What's more, increasing the size of the sudoku, in particular to 16 by 16, made generation almost impossible, as it was too resource-intensive for the machines, with resolution times sometimes exceeding 30 seconds for a 16 by 16 sudoku.
I then turned my attention to the backtracking solution and the problems of satisfying algorithmic constraints. Backtracking is a specific type of programming for solving constraint problems, which consists in testing possibilities and, if a solution cannot be found, going back to the most recent problem to test another solution (See Figure above). In theory, backtracking avoids time-consuming generation. We have therefore created a program corresponding to this category of algorithms, using the lessons and examples we found. The backtracking solution proved more efficient both in terms of time and resource consumption. The generation of a complete 16-by-16-square sudoku is of the order of a tenth of a second. However, this algorithm was not very efficient when generating larger numbers, such as a 25 by 25 sudoku matrix. The resolution time was then in excess of 30 seconds, which is not acceptable for a mobile application.
My research turned to the work of Donald Knuth and sudoku generation algorithms inspired by the Dancing Links algorithm, a recursive search algorithm using trace feedback. However, this solution remained recursive and presented major difficulties when it came to generating a random grid.
For many reasons the backtracing algorithm seemed to be the best solution for Sudozzle.




